
"Orthogonal Array-Based Latin Hypercubes".
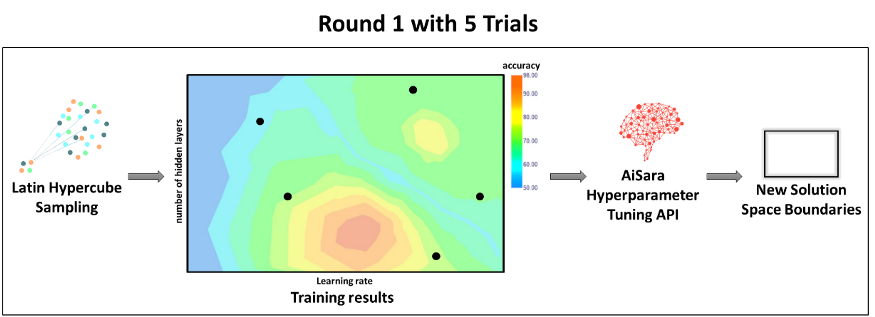
Latin hypercube sampling (program user's guide). Introduction, input variable selection and preliminary variable assessment". "An approach to sensitivity analysis of computer models, Part 1. "New approach to the design of multifactor experiments". "A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code". Thus, orthogonal sampling ensures that the set of random numbers is a very good representative of the real variability, LHS ensures that the set of random numbers is representative of the real variability whereas traditional random sampling (sometimes called brute force) is just a set of random numbers without any guarantees. All sample points are then chosen simultaneously making sure that the total set of sample points is a Latin hypercube sample and that each subspace is sampled with the same density. In orthogonal sampling, the sample space is divided into equally probable subspaces.Such configuration is similar to having N rooks on a chess board without threatening each other. In Latin hypercube sampling one must first decide how many sample points to use and for each sample point remember in which row and column the sample point was taken.One does not necessarily need to know beforehand how many sample points are needed. In random sampling new sample points are generated without taking into account the previously generated sample points.In two dimensions the difference between random sampling, Latin hypercube sampling, and orthogonal sampling can be explained as follows: Another advantage is that random samples can be taken one at a time, remembering which samples were taken so far. This sampling scheme does not require more samples for more dimensions (variables) this independence is one of the main advantages of this sampling scheme. When sampling a function of N, to be equal for each variable. A Latin hypercube is the generalisation of this concept to an arbitrary number of dimensions, whereby each sample is the only one in each axis-aligned hyperplane containing it. In the context of statistical sampling, a square grid containing sample positions is a Latin square if (and only if) there is only one sample in each row and each column.
Latin hypercube sampling python manuals#
Detailed computer codes and manuals were later published.
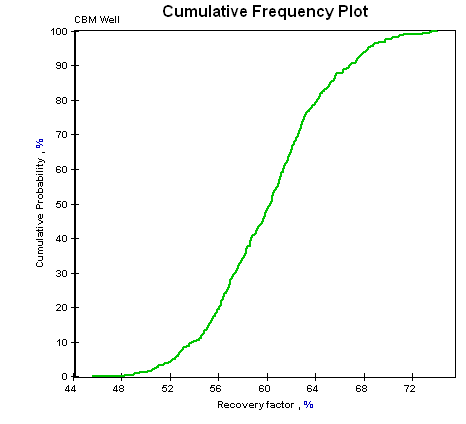
An independently equivalent technique was proposed by Eglājs in 1977. LHS was described by Michael McKay of Los Alamos National Laboratory in 1979. The sampling method is often used to construct computer experiments or for Monte Carlo integration. The computer program is user-friendly and written in FORTRAN 77 to facilitate portability.Latin hypercube sampling ( LHS) is a statistical method for generating a near-random sample of parameter values from a multidimensional distribution. If the computer model output has an associated time or spatial history then the computer program will generate a graph of the coefficients over time or space for each input-variable, output-variable combination of interest, thus indicating the importance of each input over time or space. Relationships between the coefficients and differences in their interpretations are identified. The coefficients provide alternative measures of the relative contribution (importance) of each of the various inputs to the observed output variations. These coefficients can be calculated on either the original observations or more » on the ranks of the original observations. The present computer program calculates the partial correlation coefficients and/or the standardized regression coefficients from the multivariate input to, and output from, a computer model. In particular, this program is most useful in analyzing input-output relationships when the input has been selected using the Latin hypercube sampling program developed at Sandia (Iman and Shortencarier, 1984). The computer program is designed to be used in conjunction with sensitivity analyses of complex computer models. This document is for users of a computer program developed by the authors at Sandia National Laboratories.


 0 kommentar(er)
0 kommentar(er)
